refavu.blogg.se

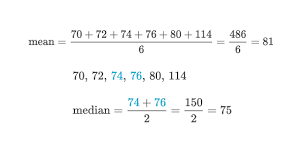
Constructing a median of a triangle with compass and straightedge animated demonstration.Medians of a triangle With interactive animation.Area of Median Triangle at cut-the-knot.Medians and Area Bisectors of a Triangle.↑ Leung, Kam-tim and Suen, Suk-nam "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp.↑ Benyi, Arpad, "A Heron-type formula for the triangle", Mathematical Gazette 87, July 2003, 324–326.↑ Boskoff, Homentcovschi, and Suceava (2009), Mathematical Gazette, Note 93.15.↑ 5.0 5.1 Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp.To find the value halfway between them, add them together and divide by 2: 21 + 23 44. E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108. In this example the middle numbers are 21 and 23. There are four medians, and they are all concurrent at the centroid of the tetrahedron. A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median of the tetrahedron. It is also called the 50 percent income, which means half of the employees work above this median salary, while half of them work below it. Median salary enables employees to identify the middle point of their salaries in their careers. Let D be the midpoint of A B ¯ TetrahedronĪ tetrahedron is a three-dimensional object having four triangular faces. The median formula is applied in the workplace to calculate the median salary that sets a reference. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.) The three medians divide the triangle into six smaller triangles of equal area.Ĭonsider a triangle ABC.

Find all the angles of ΔABC.Each median divides the area of the triangle in half hence the name, and hence a triangular object of uniform density would balance on any median. (v) The medians of an equilateral triangle are equal in length.Įxample: The angles of a triangle ABC are in the ratio of 1 : 2 : 3. (iv) The centroid of a triangle divides each one of the medians in the ratio 2 : 1. (iii) The centroid of the triangle always lies inside of triangle. (ii) All the three medians meet at one point G (called centroid of the triangle) i.e., all medians of any triangle are concurrent. Similarly, RN and MT are also medians of DLMN. The line segment LS is said to be the median of DLMN. Let S be the mid-point of MN, then LS is the line segment joining vertex L to the mid point of its opposite side. The orthocentre of an obtuse-angled triangle lies in the exterior of the triangle.Ī line segment that joins a vertex of a triangle to the mid-point of the opposite side is called a median of the triangle.įor example, consider DLMN. The altitudes drawn on equal sides of an isosceles triangle are equal.ģ. The orthocentre of a right-angled triangle is the vertex containing the right angle.ģ. The altitude bisects the base of an equilateral triangle.Ģ. The orthocentre of an acute-angled triangle lies in the interior of the triangle.Ģ. The altitudes of an equilateral triangle are equal.ġ. Although altitude of a triangle is a line segment, but in the statement of their concurrence property, the term altitude means a line containing the altitude (line segment).ġ.

Since the altitudes of a triangle are concurrent, therefore to locate the orthocentre of a triangle, it is sufficient to draw its two altitudes.The point of concurrence of the altitudes of a triangle is called the orthocentre of the triangle. (iii) Orthocentre of the triangle may lie inside the triangle, outside the triangle and on the triangle. (ii) All the three altitudes meet at a point H (called orthocentre of triangle) i.e., all altitudes of any triangle are concurrent. (iii) The side PQ, itself is an altitude to base QR of right angled PQR in figure. (ii) AD is an altitude, with D the foot of perpendicular lying on BC in figure. (i) PS is an altitude on side QR in figure. Altitude of a triangleĪn altitude of a triangle is the line segment drawn from a vertex of a triangle, perpendicular to the line containing the opposite side. Linear boundary of the triangle is the triangle itself. The points lying inside ΔABC (i.e., cross) forms the interior of ΔABC and the points lying outside ΔABC (i.e., dots) forms the exterior of the ΔABC. Interior and exterior of a triangleĪ triangle drawn on a plane divides the plane into 3 parts interior, exterior, and the triangle itself. The side AB is called the base line of ΔABC and the angle formed at vertex C opposite the base line AB is called the vertical angle. (d) Sum of the angles of a triangle is 180°, i.e., ∠A + ∠B + ∠C = 180°.

(c) Number of angles are 3, i.e., ∠A, ∠B, and ∠C. (b) Number of vertices (i.e., initial and terminal points of sides) are 3, i.e., A, B, and C. (a) Number of sides forming ΔABC are 3, i.e., AB, BC, and CA. It is a 3-sided polygon and is named as ‘ΔABC’. What is the Median and Altitude of a TriangleĪ closed figure bounded by three line segments is called a triangle.